【初心者向け】知って得する複利の威力｜単利・複利を活用した資産形成のコツ

お金を増やすために欠かすことできないキーワードである『時間』と『金利』。

『時間』は一旦置いときますが、『金利（きんり）』には「単利（たんり）」と「複利（ふくり）」があります。

そして複利は投資において、特に重要なキーワードです。

ドイツ生まれの物理学者アルベルト・アインシュタインは次の名言を残したと言われます。

「複利は人類による最大の発明だ。知っている人は複利で稼ぎ、知らない人は利息を払う」

人生において金利を活用している人は資産が増え、単利でも資産は増えますが、その増え方は複利が圧倒します。

このアインシュタインや複利の話はＳＮＳでもよく見られますが、ここで意外かもしれない注意点があります。

それは、

1. 「アインシュタインが『複利は人類最大の発明』と言った」は嘘かも。確かな証拠が何１つもないらしい。
2. 厳密にいうと株式は複利ではない。ただし複利に似た値動きをする（複利効果）。

詳しくは別の記事で説明しますので頭の片隅におきつつ、この記事では単利と複利について解説していきます。

単利と複利を考える場合に共通する前提条件は、

• 利息（りそく（％））が決まっていて一定
• 毎年、利息分が増え、減ることはない。

これを踏まえ、両者には次のような違いがあります。

では単利／複利の詳しい説明に入るのですが、その前に、まずは金利について簡単におさらいしましょう。

金利とは

金利とは、自分のお金を他の人に預けたり商品に換えたりした場合に、その資産に対して１年間につく利息（利子）の割合・比率のことです。定期預金などでよく表される利息が金利です。

金利には単利と複利があり、利息の付き方に違いがあります。

金利、利率（りりつ）、年利（ねんり）は同じ意味と考えて良いでしょう。開始月というものはなく、お金を預けてから又は商品を買ってから１年経過時に利息がつきます。（債券は半年毎が多い）

タイミングによって金利の値が変わることもありますが、基本的には金利はある期間一定と考えます。

例えば金利１％の定期預金というのは、１００万円を預けたら１年後に１万円の利息がもらえます。

つまり残高が１０１万円となります。

預金金利１％なんて夢のような

利率はありませんけど～

単利と複利の違い

それでは単利と複利の違いをみていきましょう。

単利

単利とは、元本のみに利息がつく方式です。複数年経っても毎年の利息額は同じとなります。

単利運用した場合の口座残高は、次の式で表せます。

実際に計算すると、

このように毎年５万円が増えていきます。

単利で運用される商品としては、債券（社債や国債）があります。

複利

複利とは、元本と利息の合計（元本＋利息）に対して利息がつく方式です。

１年目の利息は単利と変わりませんが２年目からは差が出ます。

複利運用した場合の口座残高は、次の式で表せます。

実際に計算すると、

単利だと３年後の口座残高は１１５万円でしたが、複利の場合はそれより７,６２５円多くなっています。

複利で運用される商品としては、銀行預金です。

資産形成シミュレーターなるものがありますので、興味があれば使ってみて下さい。

ここで複利において、勘違いしやすい点を以下に整理します。

更に株式や投資信託は損益がマイナスになることもあるため、複利とはその性格上で異なります。

単利と複利の差

前の計算をみても分かる通り、単利と複利では、利息を再投資する複利の方が増えていく金額が少しだけ大きくなります。

ただ最初は数千円と微々たる差ですが、年を重ねるごとに大きな差となって現れます。

次のグラフは単利と複利の資産を比較したものです。

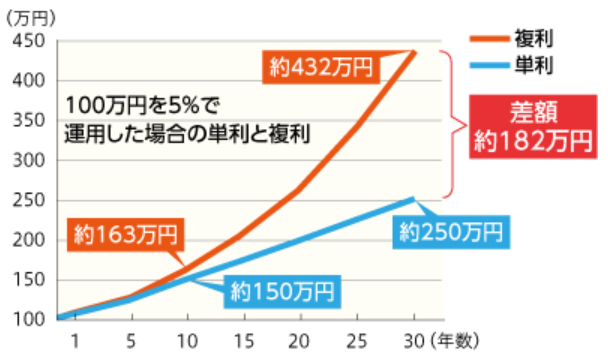
出典：三菱ＵＦＪ銀行「複利」

最初にはほとんど差が見られませんが、長期になると複利では放物線を描いて増えていきます。

１０年後の差額（１３万円）を基準で考えると、差額が２０年後時点でその５倍、３０年後で１４倍と、もの凄い勢いでその差が開いていきます。

これぞ複利が『人類最大の発明』と言われる所以（ゆえん）です。（本当のところ誰が言ったかは知りませんが・・・）

金利と利回りは違うもの

金利の話をしたので、利回りについても少し触れておきます。

金利と利回りは結果として同じ数値となる場合もありますが、基本的には異なります。

利回り

利回りとは、ある期間の損益をその期間の最初に持っていた投資元本で割った比率を指します。

言い換えると、投資金額がその期間で何％増えたかを表現するものです。利益率とも呼ばれます。（「リターン（％）」と同じとして差し支えないですが、厳密には異なります。）

損益には商品の売却益だけでなく、途中で発生した分配金なども含まれます。またここでは省略しますが、実際は手数料等も考慮する必要があります。

この式はある期間ｎ年間の利回りを示します。

金融業界では「年利」で表現する慣習があるので、これを年平均利回りに換算し直すのが一般的です。

更に年利に換算する場合、単利方式による年率換算かそれとも複利方式かによって年利回りが変わります。

先で説明したように単利では「１＋（利率）✕ｎ」、複利では「（１＋利率）^ｎ」で増えていくので、

ｎ年後の利回りは、細かい計算を省きますがこの式を活用して年数ｎで逆算すれば、単利または複利の年利回りが出てきます。

つまり金利と利回りを、その違いで表現すると次のようになります。

金利は過去に決められた値、利回りは現時点を計算した値というイメージでしょうか。

気を付けなければならいことは、損失が出た場合に利回りはマイナスとなるということです。

基本、『金利』で示される通常の金融商品において、その利率がマイナスとなることはありません。

計算例（間違い例）

ネット上で次のような説明がいくつもありましたので紹介します。

利回りを理解する上で参考にしますが、これは間違った説明です。

どこが間違いかというと、この説明は①→答え→①という単純に逆戻りの計算をしようとしているだけですが、

なぜか式①では複利で計算しているのに、②③では単利とみなし逆算しています。

そもそも逆算する必要あるの？という疑問がありますが

そこは一旦置いておきます

式①を複利で計算したら複利で元に戻せば良く、単利なら初めから単利で計算するべきです。

初めに金利３％と設定して、分配金等がなくその利率のみで増えるのであれば、単利／複利に関係なく、逆算した利回りも最初に決めた金利と同じ３％です。

計算をただ逆に戻すだけなので、同じ道を行って帰って、最初に戻ってくるだけです。

この間違った説明では、単利より複利の方が凄いよと説明する意図だと思われます。

ならば「複利運用したものを仮に単利として利回りを計算した場合」という注意書きが必要です。

なんのこっちゃ？？？

やはり説明として無理があります。

まとめ

単利と複利の違いは簡単なようで複雑ですね。

また調べていくうちに、当初の認識とは違い、いろいろなことに気づかされました。

まさかの予想外の事実が次々と判明しました。

まさかアインシュタインが

言ってなかったなんて！？

言ったかもしれないし、言ってないかもしれない・・・

どちらにせよ名言は名言ですので、今後も決して忘れることがないよう心にしっかり留めておきます。

株式もすっかり複利だと思っていましたが、複利みたいだったとは・・・

これについては↓の記事で調査／解説しています。

株式における複利効果の正体とは？金利がなくても複利が働く

まあでも結局のところの結論として、複利はやっぱり凄いということです。