アメリカで始まり、近年、日本でも話題に取り上げられるFIRE（Financial Independence, Retire Early）。
訳すと「経済的自立と早期リタイア」という意味になります。
そのFIREを実現する条件として頻繁に取り上げられるのが「４％ルール」です。
これは、リタイア時の資産を株式／債券で運用しながら、当初の資産額の４％を毎年生活費として取り崩しても、生涯を通じて資産が枯渇しないという考え方です。
言い換えれば、年間支出の25倍（4％の逆数）の資産があればFIREが可能という理論です。
しかし、このルールについて様々な意見が聞かれます。
- 大暴落が起きると実現できない？
- 相場の上下動が影響する
- インフレ率が含まれていない
- 運用商品のリターンで変わる
こうした疑問に答えるため、この記事ではEXCELを使って市場の大暴落を再現し、4％ルールの有効性を検証しました。
その検証結果は次の通りです。
- 市場の暴落は取り崩し期間にマイナスの影響を与える
- 市場が暴落→回復という低迷期だけを繰返す絶望的な状況でも、4%ルールは有効である
それでは、どのような検証を行ったのか詳しく解説していきます。
検証の条件設定
まずは検証に使用するデータなどの条件を整理します。
使用するデータを定義
計算する前に、使用するデータの設定します。
| S&P500平均リターン | 10% |
| 10年米国平均リターン | 5% |
| インフレ率 | 3% |
これらの数値は、1994年にウィリアム・ベンゲン氏が発表した論文を参考にしています。（ブログ：FIRE実現のカギを握る「4％ルール」の真実｜ウィリアム・ベンゲン氏論文を徹底解説を参照）
S&P500 引用：★S&P500 DATA
10年米国債 引用：TRADING ECONOMICS
インフレ率 引用：世界の経済のネタ帳「アメリカのインフレ率の推移」、IMF – World Economic Outlook Databases
運用資産合計のリターン設定
運用する株式と債券の配分をもとに、それらを合算した年間平均リターンを設定します。
ここでもウィリアム・ベンゲン氏の論文で取り崩し期間が最も長くなる配分である「株式75%債券25%」を採用します。
先ほどの表の数値を参考に、「株式75%債券25%」を合算した年間リターンを算出すると、
S&P500の平均リターン：10%
10年米国債平均リターン：5%より
0.75 ✕ 10% ＋ 0.25 ✕ 5% ＝ 8.75%
以降の検証では、この8.75%を年間平均リターンとして使用します。
暴落／回復を繰返すシミュレーション・モデルの設定
計算では暴落と回復をシミュレーションし、その状況で取り崩し期間がどう変わるかを検証します。検証の流れは以下です。
- 暴落の状況を作り出す
- 暴落と回復を１年おきの２年周期で繰返す
- 資産の引き出し率3～10%のそれぞれで毎年の残高を算出
- 資産残高が枯渇するまでの期間を算出する
まずここでは検証するためのモデルの設定と、それに使用する数値を準備していきます。
暴落の設定方法
まずは暴落を設定していきます。
どのくらい暴落するかですが、まだ皆さんの記憶に残っているITバブル崩壊やリーマンショックを参考にします。
これらの暴落率は、どこを起点にするかで様々な数値が紹介されていますが、おおよそ―50％付近です。
ここでは－50％の暴落と回復を繰返しながら、平均リターン8.75%を得るモデルを想定します。
シミュレーション・モデルの作成
モデルは無限のパターンを作ることができるので、ここでは暴落と暴騰を2年周期で繰り返すモデルを設定します。
次の①～③の条件で繰返すものとします。
- 1年目にマイナス50%の暴落が発生
- 2年目に回復（暴騰）して平均リターンと同じ値に戻る
- 3年目以降、①と②を繰返す
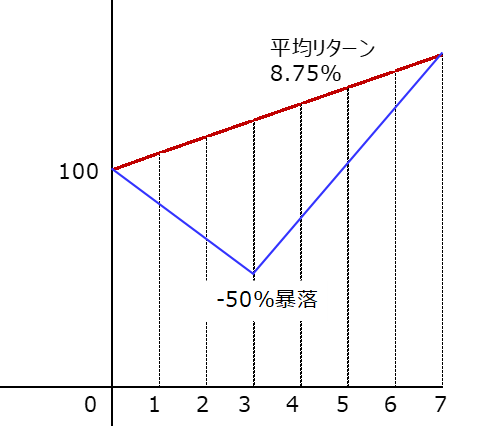
これをグラフに表したものが下の青線になります。
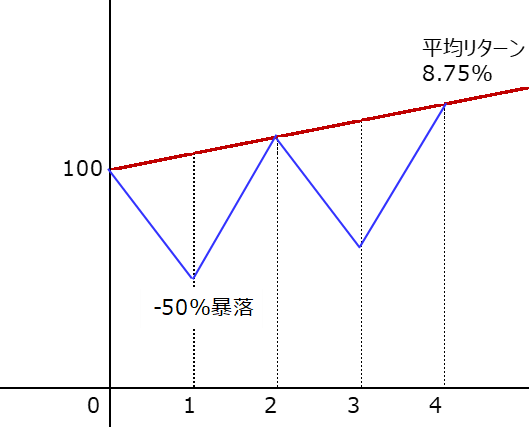
グラフは縦軸に資産額（初年度を100とする）、横軸に年数を示します。
赤線は毎年一定の平均リターン8.75%で増えた場合を示し、青線は暴落／回復を繰返しながらも平均リターン8.75%を得た場合を示します。
平均リターンより上に行かない、
かなり厳しめの設定にしています。
暴落・回復の数値設定
では次にこのモデルの青線について、市場が回復するときのリターンを求めて行きます。
前提条件として資産は複利で増えていくものとします。
複利によるn年後の資産は平均リターンをｘ、運用期間をn年とすると次の式で表せます。
元本 ✕ (1 ＋ ｘ)n
この (1 ＋ ｘ)nを計算していきます。
現在分かっているリターンの数値は次のものです。
- 0→1年の暴落：－50％
- 平均リターン： 8.75%
1→2年のリターンを求めると、
(1＋0.0875)2 ÷(1－0.5)＝ 2.36
この計算は、1→2年のリターンを求めるため、まずは0→2年の２年間のリターン(1＋0.0875)2を求め、それを0→1年のリターン (1－0.5)で割っているというものです。
分かったような
分からないような
ここは分からなくても、
なんとなくで良いです
求めた値が正しいかを、分かりやすく確認してみます。
平均リターンは8.75%なので、グラフの赤線の2年後の資産増減は、毎年の増減率を掛けて
（A）1.0875 ✕ 1.0875 ＝1.18
一方、－50％の暴落が起きる青線の2年後の資産増減は、同じように毎年の増減率を掛けて
（B）0.5 ✕ 2.36 ＝ 1.18
（A）、（B）の途中経過は異なりますが、2年後の資産増加率は「1.18」と同じになります。年平均に換算すると、共に平均リターンが8.75%で同じということです。
つまりこの（B）は、暴落／回復を繰返しながらも年平均リターン8.75%を得るモデルとなっています。
この（B）を使って計算を行っていきます。
資産が枯渇するまでの期間の算出
準備が整いましたので、検証に入っていきます。
条件の整理
これまでの内容を踏まえ、条件は以下とします。
- 資産は1000万円
- 平均リターン：8.75%
- リターンは―50%と136%を繰返す
このシミュレーションでは、資産の引き出し率（3～10％）とインフレ率（0～3％）の全ての組合せにおいて、資産が枯渇しない期間（年数）を計算します。
資産の取り崩し方法は、ウィリアム・ベンゲン氏の論文をもとに、以下のように設定します。
例えば引き出し率を4%と設定すると、
- 1年目の引き出し率は資産の4%の金額
- ２年目以降は、1年目の引き出し金額にインフレ率を考慮する
毎年の資産の4%（定率）ではない
ところが注意点です
実際のEXCELでの計算例の一部を参考で載せておきます。
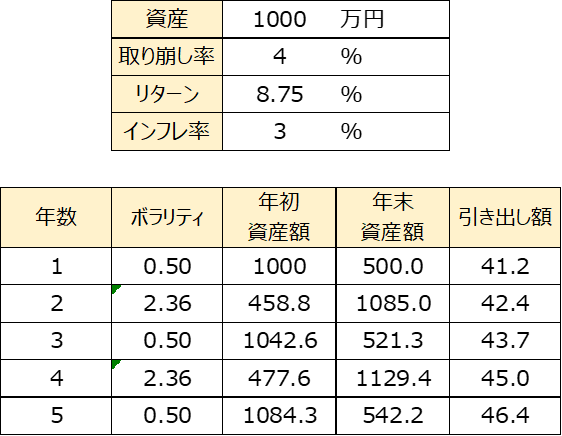
上の表が条件、
下の表が計算結果の一部です。
検証結果①（２年周期の大暴落）
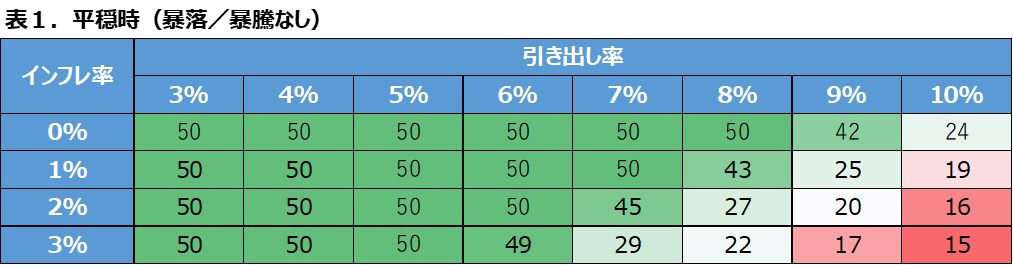
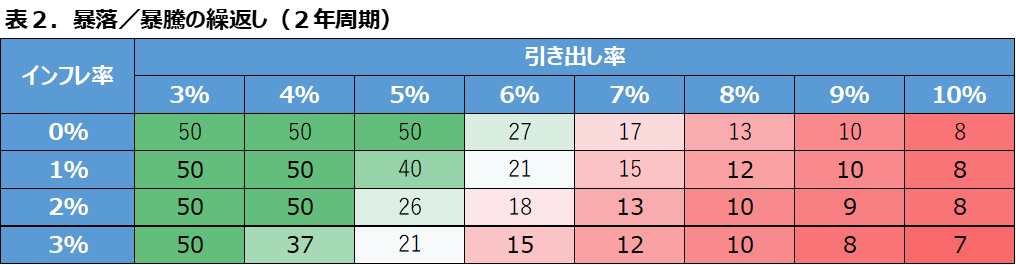
結果を表1、表2に示します。
表1は先のグラフの赤線（リターンが毎年一定）を示し、表2はグラフの青線（暴落回復を2年周期で繰返し）の検証結果を示します。
表の縦方向をインフレ率、横方向を引き出し率で区分しています。表中の数字は資産＞0円となっていた年数を表します。
この２つの表から分かることは以下のことです。
- 市場暴落は資産の取り崩し期間を大幅に減少させる
- インフレ率の上昇に伴い、取り崩し期間は短くなる
- 引き出し率が3%であれば、市場の暴落に遭遇しても資産は枯渇することなく維持できる
- 引き出し率4%も、リタイア後の資産維持の基準として採用可能である。
やはり暴落は資産の取り崩し期間に大きな影響を及ぼし、その期間を短くしてしまうようです。
もっと大きな暴落が来たら
耐えれない～
確かに未来は分かりません
ただ今回の条件は、かなり
厳しめになっています。
表2は２年周期でリーマンショック級の大暴落が発生するという、現実的にはありえないほど厳しい条件を想定しています。実際の市場環境では、仮に暴落が発生しても、表1と表２の間、更には表1に近い状況になると想定されます。
従って資産の引き出し率4%のルールは、かなり現実的であり、有効な指標といえます。
市場の大暴落というストレステストを経ても、資産の長期的な維持が可能であることが示されました。
検証結果②（7年周期の大暴落）
もう１つ異なる条件で検証します。参考とするのはITバブル崩壊です。
下のグラフの色付けした範囲で、2000年3月に発生し、2007年7月に暴落前の最高値（さいたかね）の水準まで回復しています。
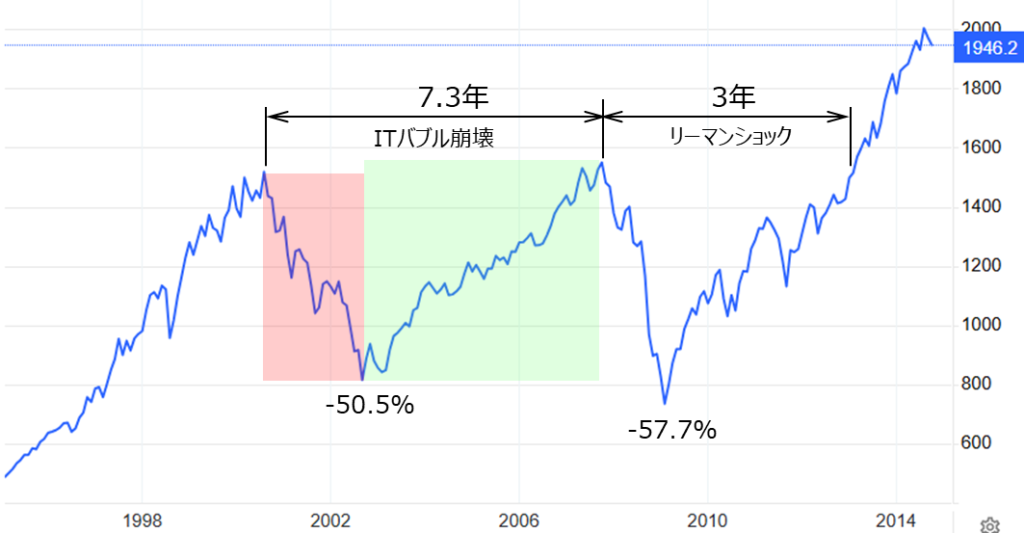
これを参考に次のモデルを想定しました。
先の2年周期で暴落・回復を繰返すモデルと違い、暴落から回復までの期間を実際の状況に合わせて7年としました。この７年を1周期として繰り返すシミュレーション・モデルを設定します。上のグラフの青線（暴落／回復を7年周期で繰返し）です。
結果は次の表3に示します。
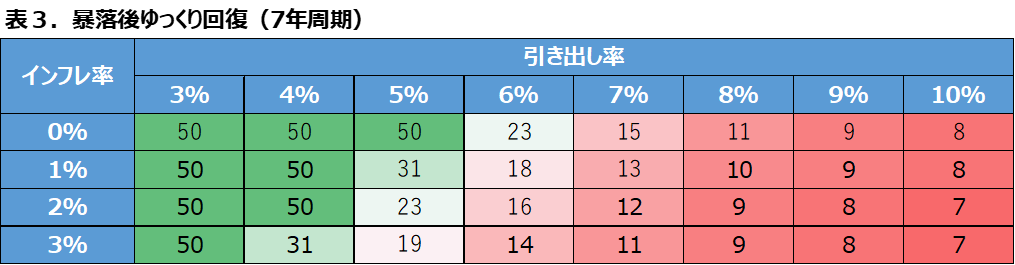
先の表2とこの表3を比較して、以下のことが分かります。
- 7年周期モデルの方が、取り崩し期間が短くなる
- 7年周期モデル方が悪化はしているが、それほど大差はない
- 数値の全体的な傾向は両モデルで同じ
取り崩し期間の年数に大差はなく、全体の傾向は同じですが、暴落している市場が低迷する期間が長いほど（赤線より下の谷の幅が広いほど）、取り崩し期間にマイナスの影響を及ぼすようです。
低迷期の谷って怖い～
広くて深い谷ほど、
恐ろしいということですね
またこの両モデルから導き出される極めて重要な結論は以下です。
たとえ市場が絶望的な低迷期だけを繰り返す、極めて厳しい条件下においても、4%の引き出し率で生涯にわたり資産を維持できる
この結論は、FIREを目指す投資家にとって、極めて重要な意味を持ちます。
2年周期の急激な暴落・回復モデルでも、ITバブル崩壊を模した7年という長期の低迷期モデルでも、4%ルールの有効性が確認されたのです。
これは、市場環境の変動パターンによらず、4%ルールが堅実な指標として機能することを示しています。
暴落時の資産残高の変化
これまでの分析では取り崩し期間に焦点を当ててきましたが、ここでは具体的な資産残高の推移を見ていきます。
下の表4は、2年周期でマイナス50%の暴落と回復を繰り返すモデル（表2）における、暴落直後かつ引き出し後の資産残高（万円）を示しています。
暴落時の資産を示しているので、その翌年は回復して、平均リターン8.75%とほぼ同じ資産残高になります。この平均リターン8.75%と同等の資産残高は、この表の数値を2.4倍すれば出てきます。
注目すべき点として、このような厳しい市場環境を想定しているにもかかわらず、資産が順調に増えていることが見て取れます。
これは市場の大きな変動に耐えながら資産を維持・成長させられることを示唆しています。
まとめ
今回検証した条件は以下の通りです。
- －50％の暴落
- 暴落を2年又は7年周期で繰り返す
これらは現実的にはあり得ないような、非常に厳しい条件で検証しました。
それでもウィリアム・ベンゲン氏が提唱した4%ルールは、リタイア後の枯渇しない資産運用の戦略として有効であることが分かります。
逆に言えば次のような備えをしておけば、4％より少し高い引出し率でも難なく生活を送れると想定できます。
- 株式／債券以外の副収入源の確保
- サイドFIREによる収入確保
- 市場暴落時の支出調整（節約）
- 長期米国債券TLTなど逆相関の資産保有
4%ルールを基本としながら、上記のような追加措置を行うことで、より高い引出し率でのリタイア生活も可能となり、さらには早期リタイア実現の可能性も高まります。
4%ルールは早期リタイアの戦略を考えるうえで、とても有効な指標であるといえます。
市場の変動に備えつつ、個々の状況に応じた安全で安定した戦略を構築することを目指しましょう。
（※税金、手数料などは考慮していませんので、最終的にはそこを加味する必要があります）
